swiftで最小限タートルグラフィック

swift playgrouds での4番目のプログラミング。今回はタートルグラフィックスの実装。

機能は最小限の LOGO　の機能で有名なタートルグラフィックスをswiftで実装した。

実装したコマンドは、以下の6つ。カラーは未実装。

• right

• left

• forward

• backward

• penDown

• penUp

これらのコマンドの組み合わせで、以下のようなグラフィックを表現できる。

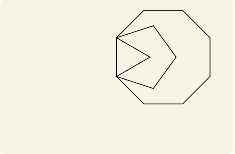
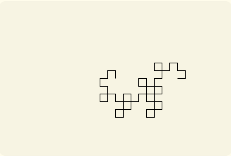
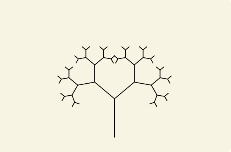
作ったクラスとその概要

ユーティリティー的なコードを除外すると、以下のような単純なコードです。

struct tinyTurtle
{
    let path             = NSBezierPath()
    var position         = CGPoint(x:0, y:0) // 絶対値での現在地
    var degree           = CGFloat(90.0)     // 角度。水平方向の右側が0度なので最初は上を向ける
    var penState         = true              // ペンを置いているか否か

    init()
    {
        self.path.move(to: position)
    }

    // 現在の方向から計回りに角度を曲げる
    mutating func right(_ degree: CGFloat)
    {
        self.degree -= degree
    }

    // 逆回転も追加
    mutating func left(_ degree: CGFloat)
    {
        right(-degree)
    }

    // 現在の位置から前進
    mutating func forward(_ length: CGFloat)
    {
        // 角度と長さと現在地から、前進後の位置を求める
        let radian   = self.degree * (CGFloat.pi / 180) //ラジアンに変換
        let vector   = length * CGPoint(x: cos(radian), y: sin(radian))
        let absPoint = self.path.currentPoint + vector

        if penState
        {
            self.path.line(to: absPoint)
        }
        else
        {
            self.path.move(to: absPoint)
        }
    }

    // バックも追加
    mutating func backward(_ length: CGFloat)
    {
        forward(-length)
    }

    // 描画用のペンの上げ下げ
    mutating func penDown()
    {
        self.penState = true
    }

    mutating func penUp()
    {
        self.penState = false
    }

    // 絶対値で示す位置へ移動 描画ポイントが迷子になっちゃうので追加
    mutating func goto(_ x: CGFloat, _ y: CGFloat)
    {
        self.position = CGPoint(x:x, y:y)
        self.path.move(to: self.position)
    }

    func draw()
    {
        self.path.stroke()
    }
}

解説は、 関東swift勉強会2017-6 で行います。

使い方

多角形を描く。

NSImage.imageWithBlock(NSSize(width:300, height:200))
{
    var t = tinyTurtle()

    t.goto(150,100)

    func poly(_ n: Int, _ size: CGFloat)
    {
        for _ in 1...n
        {
            t.forward(size)
            t.right(360.0 / CGFloat(n))
        }
    }

    poly(3, 50)
    poly(5, 50)
    poly(8, 50)

    t.draw()
}

出力結果は、以下のようになる。

ユーティリテーメソッドを利用すると、以下のようにもかける。

tinyTurtle.tinyTurtleWithBlock(NSSize(width:300, height:200))
{
    t in

    func poly(_ n: Int, _ size: CGFloat)
    {
        for _ in 1...n
        {
            t.forward(size)
            t.right(360.0 / CGFloat(n))
        }
    }

    poly(3, 50)
    poly(5, 50)
    poly(8, 50)
}

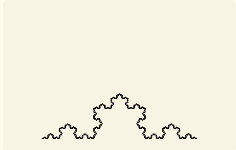
他にも、コッホ曲線を描く場合はこんな感じになります。

tinyTurtle.tinyTurtleWithBlock(NSSize(width:300, height:200))
{
    t in

    func koch(_ size: CGFloat, _ angle:CGFloat, _ n:Int)
    {
        if n == 0
        {
            t.forward(size)
            return
        }
        else
        {
            koch(size/3, angle, n-1)
            t.left(angle)
            koch(size/3, angle, n-1)
            t.right(angle * 2)
            koch(size/3, angle, n-1)
            t.left(angle)
            koch(size/3, angle, n-1)
        }
    }

    t.goto(50,20)
    t.right(90)

    koch(200, 60, 5)
}

結果は、以下のようになります。

参考文献とソースコード

プロジェクトファイル

• 　Logo 人工知能へのアプローチ

  https://www.amazon.co.jp/Logo-人工知能へのアプローチ-ラジオ技術選書-150-祐安-重夫/dp/4844301500

Previous: swiftで三段論法   Next: 落穂拾い 2017/06/26

Comments

comments powered by Disqus